タイトバインディングモデルの状態密度（３次元斜方格子）

ここでは、３次元斜方格子（直方格子）のタイトバインディングモデルでの状態密度を求めます。

１、2次元についてはこちらの記事を読まれたら幸いです。

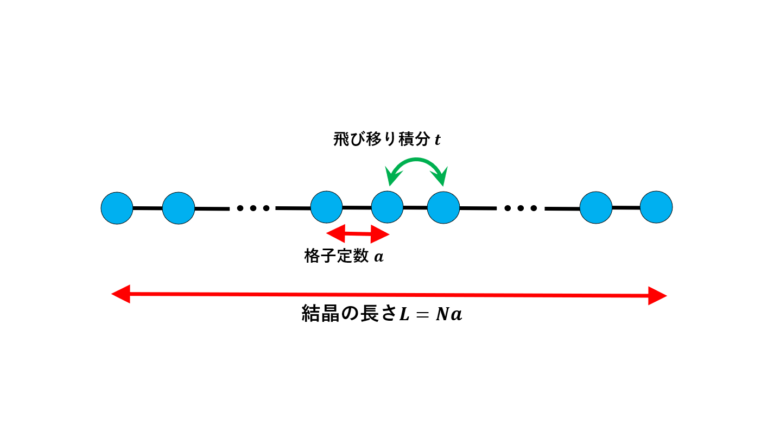
$tight_binding_1d$: タイトバインディングモデルの状態密度（１次元格子）

2023/7/4

この記事では１次元格子のタイトバインディング（tight-binding、強結合、強束縛）モデルでの状態密度を導出していきます。もともと、1,2,3次元まとめて書こうかと思ったんですが、ばか長くなる ...

物理

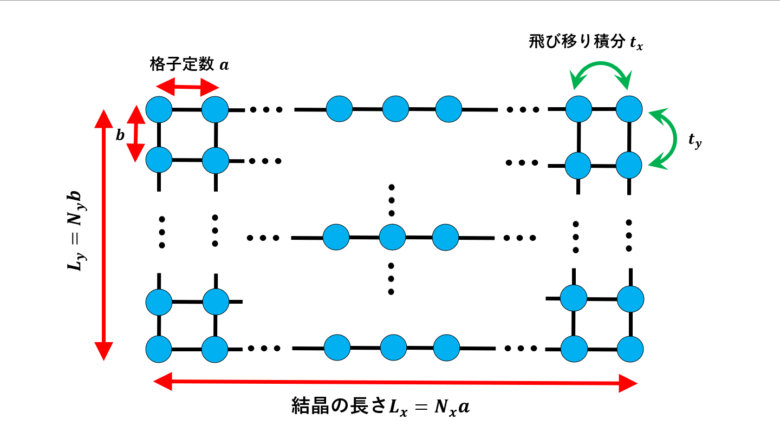
$tight_binding_2d_ja$: タイトバインディングモデルの状態密度（２次元長方格子）

2023/7/6

ここでは、２次元長方格子のタイトバインディングモデルでの状態密度を求めます。１次元についてはこちらの記事を読まれたら幸いです。（３次元はそのうち書きます）２次元長方格子のタイトバインディングモデル ...

物理

３次元斜方格子のタイトバインディングモデルの状態密度

３次元斜方格子のタイトバインディング（tight-binding、強結合、強束縛）モデルの分散関係が

$ E(k) = 2t_x \cos(k_x a ) + 2t_y \cos( k_y b ) + 2t_z \cos( k_z c )$

となることを前提知識として説明します。

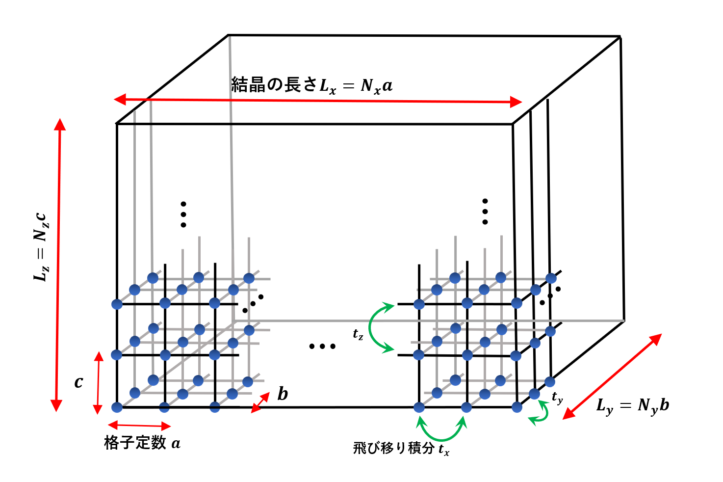
tihgt_binding_3d_ja — ３次元斜方（直方）格子のタイトバインディングモデル

ここで、簡単に見えるために、クーロン積分（原子が孤立している場合のエネルギー固有値。よく$E_0$ や $\epsilon_0$ で表されかと思います。）を基準にエネルギー $E$ を測っていることに注意です。$t_x, t_y, t_z$ は飛び移り積分（ホッピング）、$a, b, c$ は格子定数です。（上の図）

また、結晶を（周期境界条件の周期）を$ (L_x, L_y, L_z) =(N_xa, N_y b, , N_z c ) $ とし、原子の数を $N= N_x \times N_y \times N_z$ 、結晶の面積を $S= N_x a\times N_y b\times N_z c$ とします。

結論を先に申しまして、状態密度$ \frac{dN^*}{dE} $ は、

３次元斜方格子のタイトバインディングモデルの状態密度

$ \displaystyle
\frac{dN^*}{dE} =
\displaystyle \frac{2N}{\pi^3} \int_{0}^{\pi} \int_{0}^{\pi} \mathrm{Re} \left( \frac{1}{ \sqrt{ 4{t_z}^2- \left(E-2t_y \cos \kappa_y -2t_x \cos \kappa_x \right)^2 } } \right) d \kappa_x d \kappa_y
$

となります。
（$N^*$ はエネルギーが$E$以下の状態の総数。$N$ とかぶらないために∗ を付けました。）

（近々、状態密度のグラフも追加しようかと思います。）

導出が気になる方は以下も読んでくださいませ。

導出

初めに、手順は以下のようになります。

３次元波数空間の、
等エネルギー面上の面素（平行四辺形とみなせるくらい微小な面）を底面とし、
エネルギーが$ [E, E+dE) $ の範囲にある
微小直方体（下の図を見てください）の体積を求める。
その微小直方体の体積を等エネルギー面全体で足し合わせて（積分して）、
エネルギーが$ [E, E+dE) $ の範囲にある状態が占める体積$ dV^* $ を求める。
最後に、その体積 $ dV^* $ を１つの状態が占める体積 $ (2\pi)^2/S $ で割って、そん中の状態数 $ dN^* $ を求める。

ではではでは導きましょう

ここから先、$k_x, k_y$は独立変数、$k_z$ は $k_x, k_y, E$ に対する従属変数とします。つまり、

$k_z = k_z(k_x, k_y, E)$

です。もちろん$k_x$ or $k_y$ を従属変数にしてもいいです。

なぜ、$k_z$ を $k_x, k_y, E$ の関数に
（３つの波数のうち１つを、その他２つと$E$ の関数に）しなければならないのか、理由を補足しておきます。
これはなぜなら、状態密度を求めるためには、エネルギーをある値$E$ に固定して考えなければならないからです。
そうすると$k_x, k_y, k_z$ たちは、他２つの波数と相談してエネルギーが$E$ になるよう調整しなければなりません。
勝手な値はとれません。

また、対称性から、波数空間の第１象限（$k_x, k_y, k_z > 0$）の状態数だけ考えて、
それを$8$倍して全体の状態数を求めることにします。

エネルギー$dE$ 分の”殻”があるわけですが、
この殻の厚さは等エネルギー面の場所ごとに異なり、均一ではありません。

等エネルギー面の波数ベクトルが $\boldsymbol{k}=(k_x, k_y, k_z)$ である位置では、

エネルギー$dE$分の殻の厚さは $ \displaystyle \left| \nabla_{k} E \right|^{-1} dE$ となります。

なんでそうなるかは、２次元のときと全く一緒なので、そちらの記事↓（のピンクいスライドのところ）を読まれてください。

$tight_binding_2d_ja$: タイトバインディングモデルの状態密度（２次元長方格子）

2023/7/6

ここでは、２次元長方格子のタイトバインディングモデルでの状態密度を求めます。１次元についてはこちらの記事を読まれたら幸いです。（３次元はそのうち書きます）２次元長方格子のタイトバインディングモデル ...

物理

微小な直方体は図に表すと下みたいになります。

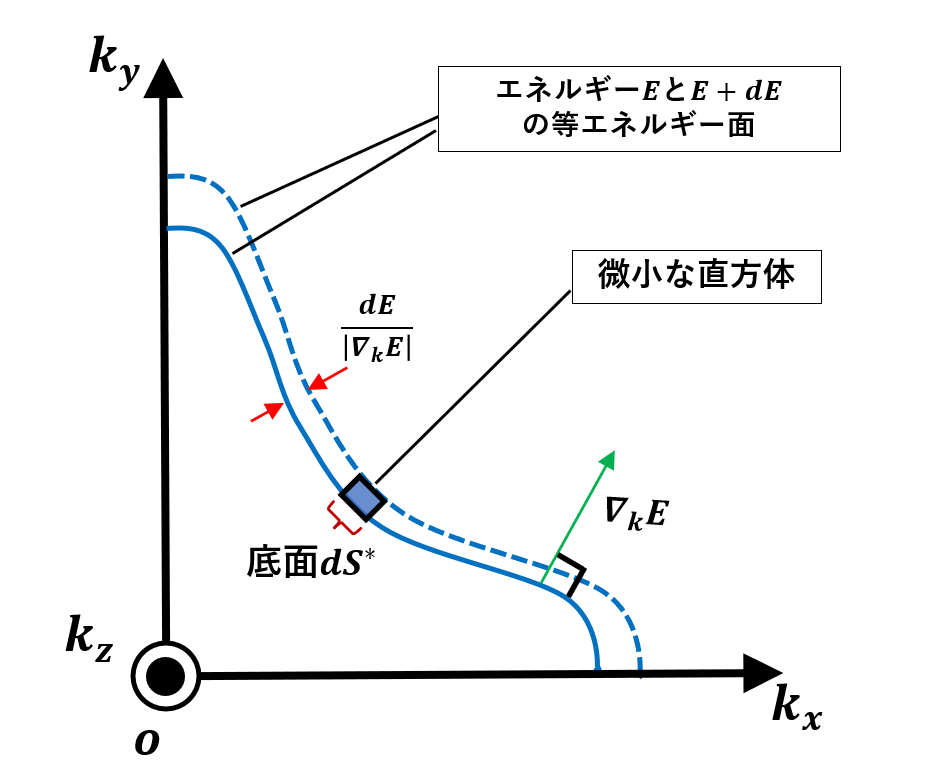
等エネルギー面の、波数の変化$dk_x, dk_y, dk_z$ 分のところにある面素$dS^*$は、2つのベクトル

$
\left( \begin{array}{c} dk_x \\ 0 \\dk_z \end{array} \right)
= \left( \begin{array}{c} 1 \\ 0 \\ \frac{\partial k_z}{\partial k_x} \end{array} \right)dk_x,
~~~\left( \begin{array}{c} 0 \\ dk_y \\dk_z \end{array} \right)
=\left( \begin{array}{c} 0 \\ 1 \\ \frac{\partial k_z}{\partial k_y} \end{array}\right) dk_y
$

が張る平行四辺形となるので、その面積$ dS^*$はそれらの外積の絶対値

$ dS^* = dk_x dk_y \left\|
\left( \begin{array}{c} 1 \\ 0 \\ \frac{\partial k_z}{\partial k_x} \end{array} \right) \times \left( \begin{array}{c} 0 \\ 1 \\ \frac{\partial k_z}{\partial k_y} \end{array}\right)
\right\|
\\ ~~~~~= dk_x dk_y\displaystyle \sqrt{ 1 + \left( \frac{ \partial k_z }{\partial k_y} \right)^2 +\left( \frac{ \partial k_z }{\partial k_x} \right)^2 }
$

となります。等エネルギー面上のエネルギー$ [ E, E+dE )$ の範囲にある状態が占める微小直方体の体積は

それらを全て足し合わせてエネルギーEの範囲にある状態が占める体積は、

となります。

ここで

はそれぞれの最小値、最大値でエネルギーによって決まります。

具体的には、条件

から決まります。

ちょいと計算してみると、

$ \displaystyle \nabla_{k} E = \left( -2t_x a \sin(k_x a), -2t_y b \sin(k_y b), -2t_z b \sin(k_z c) \right) , $

$
\displaystyle \frac{ \partial k_z }{\partial k_y} = - \frac{t_y b \sin(k_yb) }{t_z b \sin(k_z c)}
\\
\displaystyle \frac{ \partial k_z }{\partial k_x} = - \frac{t_x a \sin(k_xa) }{t_z b \sin(k_z c)}
$

となるので、微小直方体を足し合わせて（積分して）、$[E, E+dE) $ の状態が占める体積$ dV^* $ は、

$
dV^* = 2 \times \displaystyle \iint \left| \nabla_{k} E \right|^{-1} dE \times dS^{*} \\
\displaystyle \frac{dV^*}{dE} = 2 \times 8 \displaystyle
\int_{k_{y\mathrm{min}} }^{ k_{y\mathrm{max}} } \int_{k_{x\mathrm{min}} }^{ k_{x\mathrm{max}} }
\frac{1}{ 2 \sqrt{ \{ t_x a \sin(k_xa ) \}^2 + \{ t_yb \sin(k_yb ) \}^2 + \{ t_z c \sin(k_zc ) \}^2 } }
\\ ~~~~~~~~~~~~~~~~~ \times
\sqrt{ 1+ \left\{ \frac{t_y b \sin(k_yb) }{t_z c \sin(k_z c)} \right\}^2 + \left\{ \frac{t_x a \sin(k_xa) }{t_z c \sin(k_zc)} \right\}^2} dk_xd k_y $

（因子$2, 8$ はそれぞれ$\uparrow, \downarrow$ の状態と
８つの象限の状態を同時に数えていることによるものです。）

$~~~~~ = 8 \displaystyle \int_{ k_{y\mathrm{min}} }^{k_{y\mathrm{max}} }
\int_{ k_{x\mathrm{min}} }^{k_{x\mathrm{max}} } \frac{dk_x dk_y}{ |t_z |c \sin(k_zc ) } \\
~~~~~ = \displaystyle \frac{8}{c} \int_{ k_{y\mathrm{min}} }^{k_{y\mathrm{max}} }
\int_{ k_{x\mathrm{min}} }^{k_{x\mathrm{max}} }
\frac{dk_x dk_y}{ |t_z | \sqrt{ 1- \left\{ \frac{1}{2t_z} (E-2t_y \cos k_y b -2t_x \cos k_x a ) \right\}^2 } } \\
~~~~~ = \displaystyle \frac{16}{c}
\int_{ k_{y\mathrm{min}} }^{k_{y\mathrm{max}} }
\int_{ k_{x\mathrm{min}} }^{k_{x\mathrm{max}} }
\frac{dk_x dk_y}{ \sqrt{ 4{t_z}^2- \left(E-2t_y \cos k_y b-2t_x \cos k_x a \right)^2 } } \\
~~~~~ = \displaystyle \frac{16}{abc}
\int_{ \kappa_{y\mathrm{min}} }^{\kappa_{y\mathrm{max}} }
\int_{ \kappa_{x\mathrm{min}} }^{\kappa_{x\mathrm{max}} }
\frac{d \kappa_x d \kappa_y}{ \sqrt{ 4{t_z}^2- \left(E-2t_y \cos \kappa_y-2t_x \cos \kappa_x \right)^2 } }
$

（ここで、$\kappa_x=k_xa, \kappa_y = k_y b$ としました。）

$
~~~~~ = \displaystyle \frac{16}{abc} \int_{0}^{\pi} \int_{0}^{\pi} \mathrm{Re}
\left(
\frac{1}{ \sqrt{ 4{t_y}^2- \left(E-2t_y \cos \kappa_y-2t_x \cos \kappa_x \right)^2 } } \right) d \kappa_x d\kappa_y
$

この積分は(多分)できないです。

ここで、最後の行のように実部をとる関数$\mathrm{Re}$を使って考えるのを放棄したのが
$ \kappa_{x\mathrm{min}}, \kappa_{x\mathrm{max}}, \kappa_{y\mathrm{min}}, \kappa_{y\mathrm{max}} $ でして、
こいつらはそれぞれ、状態が存在する範囲での$\kappa_x=k_x a, \kappa_y=k_y b$ の最小値、最大値です。
エネルギー$ E $ によって変わります。

最後に、
求めた$ dV^* $ を状態１個当たりが占める体積$ (2\pi)^{3}/V $ で割って、
状態密度$ \frac{dN^*}{dE} $ は、

$ \displaystyle
\frac{dN^*}{dE} = \frac{dV^*}{ (2\pi)^{3}/V }
\\ ~~~~~~~=
\displaystyle \frac{2N}{\pi^3} \int_{0}^{\pi} \int_{0}^{\pi} \mathrm{Re} \left( \frac{1}{ \sqrt{ 4{t_z}^2- \left(E-2t_y \cos \kappa_y -2t_x \cos \kappa_x \right)^2 } } \right) d \kappa_x d \kappa_y
$

なげーぇ道のりでお忘れの方のためもう一度、、、

$E$はエネルギー、$t_x, t_y, t_z$は飛び移りは積分、$N$は結晶の原子の数です

ここまで読んでいただきお疲れ様ですありがとうございました。