En los viejos tiempos, pensaba
"¿Por qué no cambia la respuesta aunque se invierta la multiplicación?"
durante mucho tiempo, porque me quedé sin confianza, un día de repente, si la ley es cierta siempre.
Entonces llegué a la manera de entenderlo intuitivamente.
La ley de la multiplicación se llama "ley conmutativa", que también es cierta para la suma.
Curiosamente, esta ley conduce al hecho de que la división tiene dos significados.
Como dicen otros artículos, se puede entender la ley
si tanto el multiplicando como el multiplicador son números enteros.
¿Pero qué pasa con la multiplicación en la que el multiplicando y el multiplicador no son enteros?
En mi opinión, tenemos que pensar la siguiente pregunta para pensar si la ley es cierta para cualquier multiplicación de todos los números reales.
En primer lugar, ¿qué es "multiplicar", por ejemplo, "2 × 3"?
Tal vez puedas explicar esa expresión como
"preparar tres "2" y luego sumarlos" o "2+2+2".
Pero, ¿y si los números no son enteros, por ejemplo, "2,5 × 3,5"?
Puedo explicar esta multiplicación diciendo algo como
"hacer 3,5 visto a partir de 2,5 (considerando 2,5 como 1)".
En este caso, podemos asegurarnos de que 2,5 × 3,5 = 3,5 × 2,5 utilizando las dos figuras siguientes.
El área roja puede interpretarse como área matemática o, para ser más concretos en este mundo real, cantidad de agua en una medida.
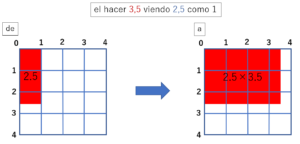
2,5×3,5
y
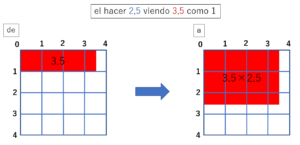
3,5×2,5
Como se puede entender intuitivamente a partir de estas cifras,
"el 3,5 al considerar el 2,5 como 1" = "el 2,5 al considerar el 3,5 como 1".
Esto significa que
2.5 × 3.5 = 3.5 × 2.5.
Según esta forma de pensar, deberías ser capaz de imaginar que la "ley conmutativa" para cualquier multiplicación de todos los números reales es cierta.