manami

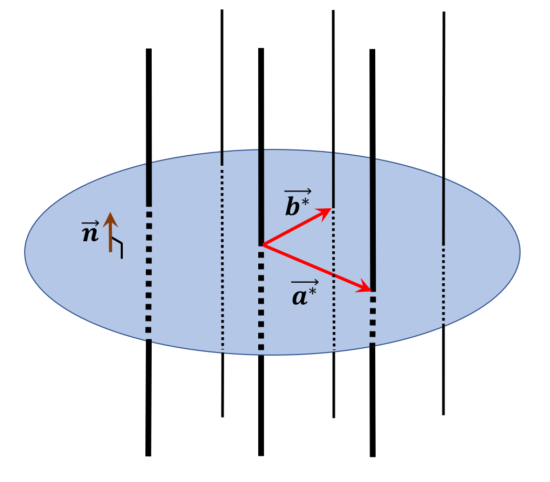
I felt the formula of the primitive translation vectors of the 2d reciprocal lattice hadn't spread out there somehow. (Neither had "reciprocal lattice rods", I thought.) So I wrote it with its derivation here. Aassuming that you already know the formula of the reciprocal lattice vectors in 3d,I shall derive that in 2d. Formulas of the reciprocal lattice vectors in 2D First, the formula of the reciprocal lattice vectors in 3d are given by \( \vec{a^*} = 2\pi \displaystyle \frac{\vec{b} \times \vec{c}}{\vec{a} \cdot (\vec{b} \times \vec{c}) } \),    \( \vec{b^*} = 2\pi \displaystyle \frac{\vec{c} \times \vec{a}}{\vec{a} \cdot (\vec{b} \times ...

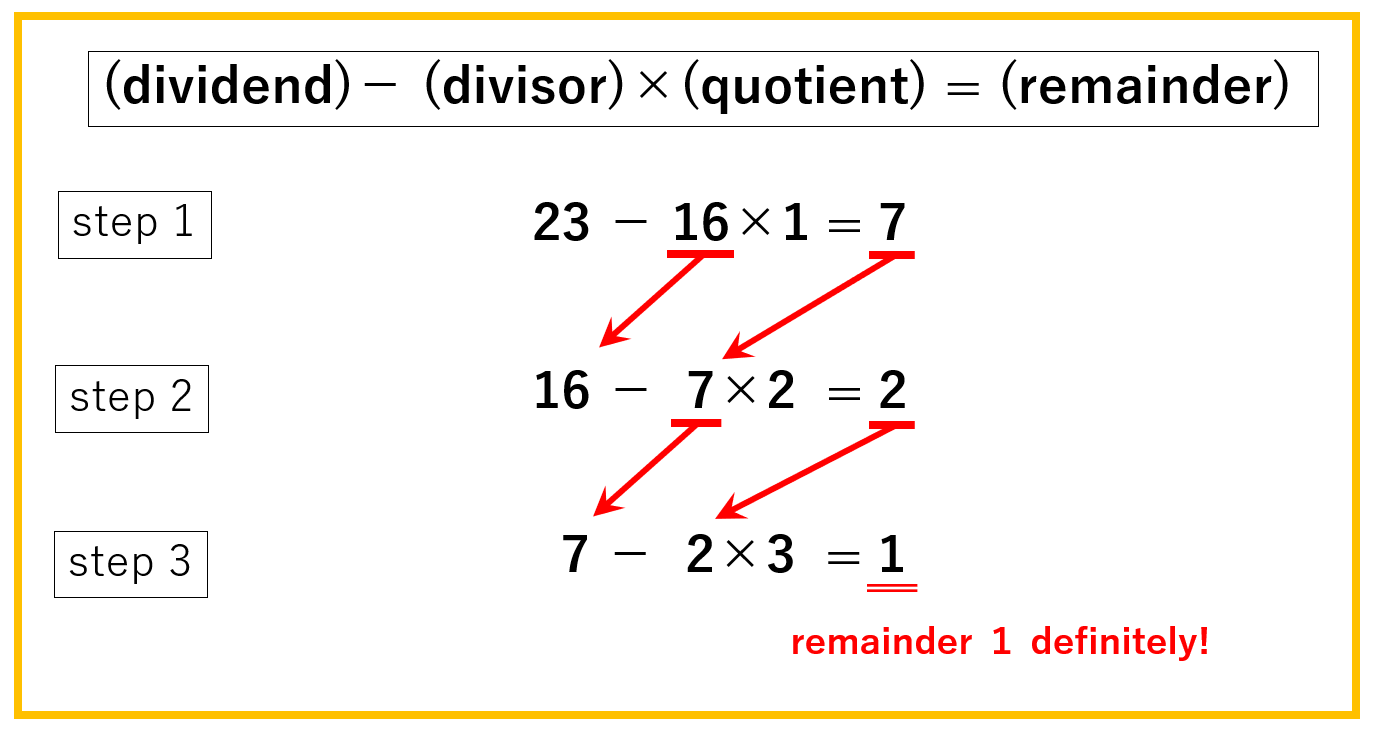
Here I wrote about why one of the integer solutions (paticular solution) of a linear Diophantine equation can be obtained by Euclidean algorithm. I hope this will help those high school students who have learned the procedure of Euclidean algorithm and can use it for the time being, but are still puzzled as to why it can be used. I hope it will be of help for such high school students. If you understand the "why," you will not forget the procedure. And if you don't remember the procedure in the first place, this article will help you remember it ...