むかしむかし、高校の化学の平衡定数\( K \) について、なぜに反応式の「係数乗」出てくんねん、
と思ったので、考えたら直観的な説明が作れました(と思います)。
あと、なかなか直観的に説明している記事無さそうかなーと思って、ここに書いて共有させてもらうことにしました。
理論の道筋を、ゴールからスタートへ逆にたどる感じ(うまく言えない)にしました。具体的には
- 平衡定数とはなんだったか紹介
- 「反応速度」を紹介、そいつから平衡定数を導出
- なぜ「反応速度」が「係数乗」に比例するのか
という順番です。
平衡定数 \(K \) とは
何はともあれ平衡定数 \(K\) の定義を復習しましょう。以下のような反応を考えます。
\( \alpha \mathrm{A} + \beta \mathrm{B} \rightleftharpoons \gamma \mathrm{C} + \delta \mathrm{D} \)
(ここでは、多段階反応などの複雑な話はしません、。そもそも高校でやったっけ)
矢印の右向きに進む(AとBからCとDができる)反応を正反応、
それに対して左向きに進む反応を逆反応とします。
これに対して平衡定数 \(K\) は、
\( K = \displaystyle \frac{ [\mathrm{A}]^{\alpha} [\mathrm{B}]^{\beta} }{ [\mathrm{C}]^{\gamma} [\mathrm{D}]^{\delta} }\)
と表され、温度に依存するけど、温度さえ一定なら定数であると習うはずです。
反応速度と平衡定数
まず、「反応速度」というのを知る必要があります。まずは、その式から、平衡定数\( K \) を導出し、その後でなぜ反応速度が係数乗を含むのかを説明します。
正反応(forward reaction)の速度 \( v_f \) は以下の式で表せます。
\( v_f = k_f \displaystyle [\mathrm{A}]^{\alpha} [\mathrm{B}]^{\beta} \)
\( v_f \) はより具体的には、単位時間(例えば1秒間)あたりに起こる
「\(\alpha\) 個のA原子と\(\beta\) 個のB原子から、\(\gamma\) 個のC原子と\(\delta\) 個のD原子が生まれる」
の回数を表します。
または、それをアボガドロ数\(N_\mathrm{A} \) で割ってmol 単位にすることが多いかもしれません。
なので、\( v_f \) の単位は「/s」や「mol/s」とすればいいでしょう。
また、\( k_f\) は、大学で習うんですが、「反応速度定数」と呼ばれ、温度に依存します。これは、衝突が起こった時、反応が起こる確率に比例するものであると考えていいでしょう。
その確率は温度に依存するんですが、それを考えるにはどうしても大学の知識が必要になります。(てか大学でも本当のガチの理屈までは習わないかと思います。)
逆反応(reverse reaction)の反応速度\( v_r \)に関しても同様に
\( v_r = k_r \displaystyle [\mathrm{C}]^{\gamma} [\mathrm{D}]^{\delta} \)
です。平衡状態とは、反応に関わる分子の数が変化しなくなった状態のことだったので、
そのためには正反応と逆反応の反応速度が等しいこと、つまり \( v_f = v_r \)、つまり
\( k_f \displaystyle [\mathrm{A}]^{\alpha} [\mathrm{B}]^{\beta}= k_r \displaystyle [\mathrm{C}]^{\gamma} [\mathrm{D}]^{\delta} \)
が成り立つことになります。これを変形して、
\( \displaystyle \frac{ [\mathrm{A}]^{\alpha} [\mathrm{B}]^{\beta} }{ [\mathrm{C}]^{\gamma} [\mathrm{D}]^{\delta} }
= \frac{k_r}{k_f } =: K\)
(\( =: \) は「左辺で右辺を定義する」という意味)というわけです。
では、なんで \( v_f, v_r \) はあんな風な式で表されるんでしょう?
なぜ反応速度に係数乗?
これを理解するため、そもそも化学反応はどのように起こるか想像してみると、
分子が飛び回っていて、反応に必要なだけの分子が「衝突」したときに、化学反応が起こる
のだと、頭の中にそのシーンを浮かべることができたでしょうか。
実際には「衝突」しただけで必ず反応が起こるわけではなく、「衝突」したときに反応が起こる確率も考慮しなければなりません。
以上から、正反応の反応速度\( v_f \)(単位時間に反応が起こる回数)は、
\( v_f = \left( \begin{array}{c}
\text{単位時間に起こる} \\ \text{反応に必要なだけの} \\ \text{分子の衝突回数}
\end{array}
\right)
\\ ~~~~~~~~~~\times \left(
\begin{array}{c}
\text{衝突したときに} \\
\text{反応が起こる確率}
\end{array} \right)
\)
だと直観的に想像できるのではないでしょうか。
「衝突したときに反応が起こる確率」が反応速度定数 \( k_f \) に対応しますので、あとは
\( \left( \begin{array}{c}
\text{単位時間あたりの}
\\ \alpha \text{個以上のAと} \\ \beta\text{個以上のB} \\
\text{の衝突回数}
\end{array}
\right)
\propto [\mathrm{A}]^{\alpha} [\mathrm{B}]^{\beta}
\)
であることを理解すればいいのです。
以下、説明を具体的にするために、\( \alpha = 2, \beta = 1 \) の場合を考えます。
まず、下の図を見てみましょう。
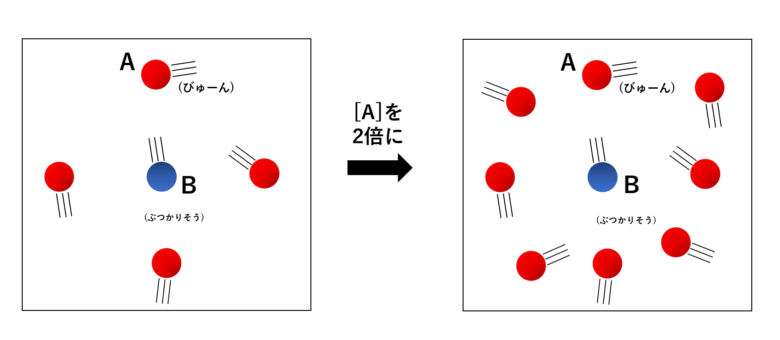
\( \mathrm{A} \)の濃度 \( [\mathrm{A}] \) を2倍にすると、\( \mathrm{A} \) と \( \mathrm{B} \) が2倍の確率で衝突しそうになっていて、
同様にを3(4, 5, ...)倍の濃度を頭の中で想像してみると、3(4, 5, ...)倍の確率で衝突しそうになりそうだと感じられるのではないかと思います。
よって、\( \mathrm{B} \) が \( \mathrm{A} \) と(1個以上の\(\mathrm{A} \)と)衝突する頻度は、\( [\mathrm{A}] \) に比例する
と考えられます。続けて、下の2枚目の図を見てみましょう。
今度は、\( \mathrm{B} \) が 1個以上の \( \mathrm{A} \) と衝突していることを前提とした場面を考えています。
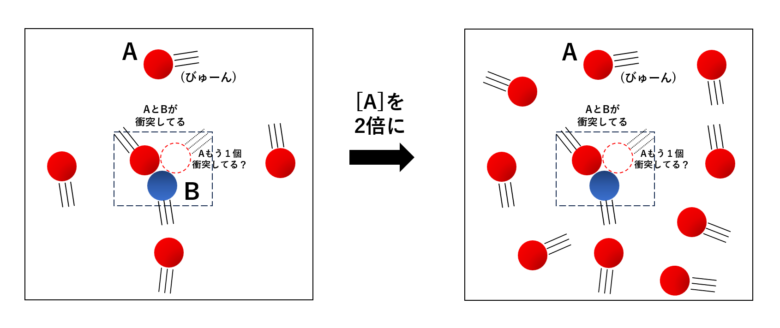
その場合のうち、\( \mathrm{B} \) が 2個以上の \( \mathrm{A} \) と衝突している確率を考えると、それもまた
\( [\mathrm{A}] \) を2(3, 4, ...)倍にすると、2(3, 4, ...)倍になりそうです。
よって、1個の\( \mathrm{A} \) と衝突している \( \mathrm{B} \) が、 もう1個以上の\(\mathrm{A}\)と衝突する頻度は、\( [\mathrm{A}] \) に比例する
と考えられます。けっきょく、
\( \mathrm{B} \) が2個以上の\(\mathrm{A}\)と衝突する頻度は、
1個の\(\mathrm{A}\) と衝突した上でさらにもう一個以上の\(\mathrm{A}\)と衝突している頻度なので、
\( [\mathrm{A}] \times [\mathrm{A}]=[\mathrm{A}]^2 \) に比例する
と考えられます。
同様にして、衝突している2個の\(\mathrm{A} \)と1個以上の\(\mathrm{B} \) が衝突する頻度は、\( [\mathrm{B}] \) に比例します。
以上から、
\( \left( \begin{array}{c}
\text{単位時間あたりの}
\\ 2 \text{個以上のAと} \\ 1 \text{個以上のB} \\
\text{の衝突回数}
\end{array}
\right)
\propto \displaystyle [\mathrm{A}]^{2} [\mathrm{B}] \)
が導かれ、比例定数を\( k_f \) としたものが「反応速度式」
\( v_f = k_f \displaystyle [\mathrm{A}]^{2} [\mathrm{B}] \)
となるわけです。
\(\alpha ≧ 3\) や \(\beta ≧ 2\) のときや、\(v_r\) のほうに関しても同様にして考えられます。
まとめおまけ
いい加減にまとめますと、
反応速度\( v_f, v_r \) が濃度の「反応式の係数乗」に比例することを頑張って理解すれば、
平衡状態では正反応、逆反応の速度が等しい(\( v_f = v_r \))ということから
平衡定数が反応速度定数の比として定義できる(\( K := \frac{k_r}{k_f} \))
でした。
ちなみに、多段階反応でも1段階ごとの反応(素反応)に対しては
同じ風に平衡定数は定義できますね。
一般には同じ方法では定義できなさそうですけど。
でも、ある条件を満たす多段階反応であれば、同じように、
最初の反応物と最後の生成物の濃度の「係数乗」だけで
平衡定数が定義できそうです。
どんな多段階反応でそうできるそうか、考えてみてください。数学的に。
そうできない場合は、また大学に行って考えましょう。
読まれてくださって、ありがとうございます。お疲れ様です。