I gamle dager tenkte jeg
«Hvorfor endres ikke svaret selv om multiplikasjonen er reversert?»
for lenge, for jeg ble usikker, en dag plutselig, om loven er sant når som helst.
Så nådde jeg måten å forstå det intuitivt.
Loven om multiplikasjon kalles «kommutativ lov», som også gjelder for tilegg.
Interessant, denne loven fører til det faktum at divisjon har to betydninger.
Som andre artikler sier, kan du kanskje forstå loven hvis både multiplikanden og multiplikatoren er heltall.
Men hva med multiplikasjon der multiplikanden og multiplikatoren ikke er heltall?
Etter min mening må vi tenke følgende spørsmål for å tenke om loven gjelder for enhver multiplikasjon av alle reelle tall.
For det første, hva er «multiplikasjon», for eksempel «2 × 3»?
Du kan være i stand til å forklare det ordtaket som «å forberede tre 2-tall og deretter legge dem sammen» eller «2 + 2 + 2».
Men hva hvis tallene ikke er heltall, for eksempel «2,5 × 3,5»?
Jeg kan forklare dette multiplikasjonsuttrykket slik «å lage 3,5 sett fra 2,5 (når du betrakter 2,5 som 1)».
Her kan vi sørge for at 2,5 × 3,5 = 3,5 × 2,5 ved hjelp av de to figurene nedenfor.
Det røde området kan tolkes som matematisk areal eller, for å være mer spesifikk i denne virkelige verden, vannmengde i et mål.
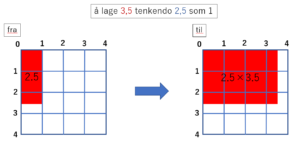
og
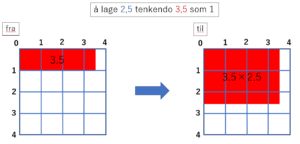
Som du kan forstå intuitivt fra disse figurene,
«de 3,5 når man betrakter 2,5 som 1» = «de 2,5 når man betrakter 3,5 som 1»,
Dette betyr at
2.5 × 3.5 = 3.5 × 2.5.
I henhold til denne måten å tenke på, bør du kunne forestille deg
at den «kommutative loven» for enhver multiplikasjon av alle reelle tall er sann.