I felt the formula of the primitive translation vectors of the 2d reciprocal lattice hadn't spread out there somehow. (Neither had "reciprocal lattice rods", I thought.)
So I wrote it with its derivation here.
Aassuming that you already know the formula of the reciprocal lattice vectors in 3d,
I shall derive that in 2d.
Formulas of the reciprocal lattice vectors in 2D
First, the formula of the reciprocal lattice vectors in 3d are given by
\( \vec{a^*} = 2\pi \displaystyle \frac{\vec{b} \times \vec{c}}{\vec{a} \cdot (\vec{b} \times \vec{c}) } \), \( \vec{b^*} = 2\pi \displaystyle \frac{\vec{c} \times \vec{a}}{\vec{a} \cdot (\vec{b} \times \vec{c}) } \), \( \vec{c^*} = 2\pi \displaystyle \frac{\vec{a} \times \vec{b} }{\vec{a} \cdot (\vec{b} \times \vec{c}) } \).
( ofc, \( \vec{a}, \vec{b}, \vec{c} \) and \( \vec{a^*}, \vec{b^*}, \vec{c^*} \) are the primitive translation vectors of the real lattice and those of the reciprocal lattice, respectively )
The lattice in 2d can be regarded as
that in 3d one of whose primitive translation vectors has infinite length
(or, in other words, which has an infinite period in a certain direction).
Therefore, by \( \| \vec{c} \| \rightarrow \infty \), (or rathar, you had better think like this to be conscious of the concept of "reciprocal lattice rods")
you can obtain the 2d reciprocal lattice vectors as follows.
Formulas of 2d Reciprocal Lattice Vectors
\( \vec{a^*} = 2\pi \displaystyle \frac{\|\vec{b} \|^2 \vec{a} ~ - ~ (\vec{a} \cdot \vec{b}) \vec{b}}{\| \vec{a} \times \vec{b} \|^2},
\\ \vec{b^*} = 2\pi \displaystyle \frac{\|\vec{a} \|^2 \vec{b} ~-~ (\vec{a} \cdot \vec{b}) \vec{a}}{ \| \vec{a} \times \vec{b} \|^2}. \)
Ofc, \( \vec{a^*} \cdot \vec{a} = \vec{b^*} \cdot \vec{b} = 2 \pi,~~~ \vec{a^*} \cdot \vec{b} = \vec{b^*} \cdot \vec{a} = 0 \) are satisfied.
If you are interested in its more datailed derivation or what "reciprocal lattice rods" are, please read the following, and I'll appreciate you.
The derivatoin of the 2d formula
and what "reciprocal lattice vectors" are
Before \( \| \vec{c} \| \rightarrow \infty \), first of all,
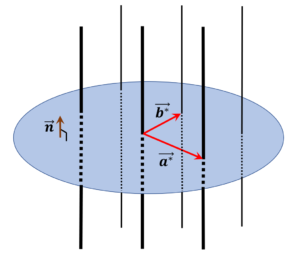
I shall express \( \vec{c} \) as the sum of its projection on the three linearly independent vectors, \( \vec{a}, \vec{b}, \vec{a} \times \vec{b} \).
\( \vec{c} = \alpha ~\vec{a} + \beta ~\vec{b} + L ~\vec{n} \).
Here, \( \vec{n} = \displaystyle \frac{ \vec{a} \times \vec{b} }{ \|\vec{a} \times \vec{b}\| } \) is a unit vector perpendicular to the plane
which includes \( \vec{a}\) and \(\vec{b} \).
Then substituting this \( \vec{c} \) into the expression of \( \vec{a^*}, \vec{b^*}, \vec{c^*} \), you can obtain
\( \vec{a^*} = 2\pi \displaystyle \frac{\|\vec{b}\|^2 \vec{a} ~-~ (\vec{a} \cdot \vec{b}) \vec{b}}{\| \vec{a} \times \vec{b} \|^2} ~ + ~ 2\pi \frac{\alpha}{L}~\vec{n} \),
\( \vec{b^*} = 2\pi \displaystyle \frac{\|\vec{a}\|^2 \vec{b} ~-~ (\vec{a} \cdot \vec{b}) \vec{a}}{\| \vec{a} \times \vec{b} \|^2} ~-~ 2\pi \frac{\beta}{L}~\vec{n} \) ,
\( \vec{c^*} = \displaystyle \frac{2\pi}{L} \vec{n} \).
Here, I used a formula for vector calculas,
\( \vec{A} \times (\vec{B} \times \vec{C}) = (\vec{A} \cdot \vec{C})~\vec{B} ~-~ (\vec{A} \cdot \vec{B})~\vec{C} \)
and so on.
If \( L\) is infinitely big, in other words, \( \|\vec{c}\| \rightarrow \infty \) is given,
( It doesn't matter whether \(\alpha, \beta \) are infinitely big or not)
\( \vec{c^*} \) is an infinitely short(length=0) primitive translation vector with the direction of \( \vec{n} \).
Then, the reciprocal lattice by the primitive translarion vectors in 3d of the above expressioin \( \vec{a^*}, \vec{b^*}, \vec{c^*} \)
is lattice lines? rather than lattice points, or is a gathering of lines..
Those guys are called "reciprocal lattice rods".
When it comes to crystal structure analysis by electron or X-ray diffraction,
when the scattering vector \( \Delta \vec{k} = \vec{k'} - \vec{k} \) of the incident electron or X-ray to the 2d sample
is equal to the vector corresponding to the arbitary point on the reciprocal lattice rods,
the diffraction with the \( \Delta \vec{k} \) occurs.
(People who came along from the band theory to this article don't have to understand what this above statemant is getting at, well, maybe, I guess.)
And then, the 2d formulas of \( \vec{a^*}, \vec{b^*} \) written in one of the earlier entries here
\( \vec{a^*} = 2\pi \displaystyle \frac{\|\vec{b}\|^2 \vec{a} ~ - ~ (\vec{a} \cdot \vec{b}) \vec{b}}{\| \vec{a} \times \vec{b} \|^2} \), \( \vec{b^*} = 2\pi \displaystyle \frac{\|\vec{a}\|^2 \vec{b} ~-~ (\vec{a} \cdot \vec{b}) \vec{a}}{\| \vec{a} \times \vec{b} \|^2} \)
are the primitive translation vectors
of the 2d latttice which you can obtain by cutting the reciprocal lattice rods vertically (with the plane which includes \( \vec{a}, \vec{b}\)).
Also, btw, when it comes to the band theory, simply
you can take it that the 2d formula is
of those extracted from the wavenumber vectors in the reciprocal lattice rods,
on the condition "crystal momentum perpendicular to the 2d plane"=0,
as Bloch wavenumbers.
If you find my mistakes and comment about them, I'm glad n appreciate you..,,,,.,.,..