昔、僕が高校3年生のときに、三次関数と直線が囲む面積を求める積分はどうにか楽にならないかと思って先生に何か裏ワザ的な、公式的なが無いか聞きました。
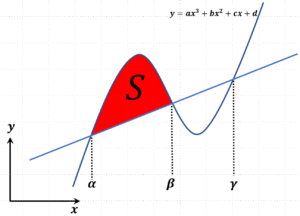
下図の赤い部分の面積\( S \)のことでして、
あの有名な「1/12公式」(三次関数版) は使えません。
公式無いよーと言われたんですけど、疑って頑張ったら作れました。
Web検索してもその公式が出てこなかったので、わー僕しか知らないイエーイって歓喜してました。そしたら他の数学の先生が、あー昔、他の人がそんな式出しとったねーって言ってきたので、僕はとても残念がりました。なつかしい
三次関数と直線が囲む面積の公式
上図の赤い部分の面積\( S \)を計算するためには、とりあえずまず、(三次関数) = (直線の式) という方程式を立て、移項、因数分解などして、
\( a(x-\alpha) (x-\beta) (x-\gamma) = 0 \)
という形に変形して、交点 \( \alpha, \beta, \gamma \) を求めますね。
その後、その左辺の因数分解された式を \( \alpha ≦ x ≦ \beta \) の範囲で積分すれば、面積\( S \)が求められますね。
(ここまでのことを読者様が理解している前提で書きます。)
そこで次の公式の出番です。
三次関数と直線が囲む面積の公式
センター試験のときの検算に大いに活躍してくれましたよ。
(昔は"共通テスト"じゃなくて"センター試験"だったのだよ)
もちろん、\(\gamma = \beta \) とすれば、あの「1/12公式」(三次関数版)になります。
ところでこれなんて呼べばいいんですかね。「1/12公式」という名前はもう使われていますし。これも1/12入ってるんですけどね。
「一般1/12公式」はどうでしょう?
言うまでもないかもしれませんが、上図で \( \alpha≦ \beta ≦ \gamma \) となっていて、\( \beta ≦ x ≦ \gamma \) の範囲の三次関数と直線の式を求めるのにも使えます。
上の公式で \( \alpha \rightarrow \beta, ~~\beta \rightarrow \gamma \) と置き換えるだけですね。
導出
三次関数の \(x^3\) の係数 \(a\) は省いて、
\( \displaystyle \int_{\alpha}^{\beta} (x-\alpha) (x-\beta) (x-\gamma) dx
\\ ~~= \displaystyle \frac{1}{12} (\beta - \alpha) ^3 (2\gamma - \beta -\alpha) \)
であることを導出します。
途中で「1/12公式」、
\( \displaystyle \int_{\alpha}^{\beta} (x-\alpha) (x-\beta)^2 dx
=~ \frac{1}{12} (\beta - \alpha)^4 \)
と二次関数の積分の「1/6公式」
\( \displaystyle \int_{\alpha}^{\beta} (x-\alpha) (x-\beta) dx
=~ -\frac{1}{6} (\beta - \alpha)^3 \)
を使います。ここで符号に注意しましょう。なぜ2つの公式でそれぞれ、ー(マイナス符号)が付かない、付くのかは、被積分関数(\(\int dx\)の中身 )のグラフを思い浮かべれば、理解できるかと思われます。
では、導出します。
\( \displaystyle \int_{\alpha}^{\beta} (x-\alpha) (x-\beta) (x-\gamma) dx \)
\( = \displaystyle \int_{\alpha}^{\beta} x (x-\alpha) (x-\beta) dx
\\~~~~~ \displaystyle - \gamma \int_{\alpha}^{\beta} (x-\alpha) (x-\beta) dx \)
(ここで、上の1項目を部分積分&2項目に「1/6公式」)
\(= \displaystyle \left[ x (x - \alpha) \cdot \frac{1}{2}(x - \beta)^2 \right]_{\alpha}^{\beta}
\\~~~~~ \displaystyle - \int_{\alpha}^{\beta} (2x-\alpha) \cdot \frac{1}{2}(x-\beta)^2 dx
\\ ~~~~~~~~~~ \displaystyle - \left\{ - \frac{1}{6} \gamma (\beta -\alpha)^3 \right\} \)
(1項目は0となる。2項目の積分を\(2x-\alpha = 2(x-\alpha) + \alpha \) による分解。)
\( = \displaystyle 0 ~ - 2 \int_{\alpha}^{\beta} (x-\alpha) \cdot \frac{1}{2}(x-\beta)^2 dx
\\~~~~~ \displaystyle + \alpha \int_{\alpha}^{\beta} \frac{1}{2}(x-\beta)^2 dx
\\~~~~~~~~~~+ \displaystyle \frac{1}{6} \gamma (\beta -\alpha)^3 \)
(ここで2項目に「1/12公式」、3項目は単純に積分)
\( = \displaystyle ~ - 2 \cdot \frac{1}{2} \cdot \frac{1}{12} (\beta- \alpha) ^4
\\~~~~~ \displaystyle + \alpha \left[ \frac{1}{6}(x-\beta)^3 \right]_{\alpha}^{\beta}
\\~~~~~~~~~~+ \displaystyle \frac{1}{6} \gamma (\beta -\alpha)^3 \)
\( = \displaystyle ~ - \frac{1}{12} (\beta- \alpha) ^4 + \frac{1}{6}\alpha(\alpha -\beta)^3
\\~~~~~~~~~~+ \displaystyle \frac{1}{6} \gamma (\beta -\alpha)^3 \)
\( = \displaystyle ~ - \frac{1}{12} (\beta- \alpha)^3 (\beta - \alpha )
\\~~~~~ \displaystyle - \frac{1}{12} (\beta - \alpha )^3 \cdot 2\alpha
\\~~~~~~~~~~+ \displaystyle \frac{1}{12}(\beta -\alpha)^3 \cdot 2 \gamma \)
\( = \displaystyle \frac{1}{12}(\beta -\alpha)^3 ( -\beta + \alpha - 2\alpha + 2 \gamma ) \)
\( = \displaystyle \frac{1}{12}(\beta -\alpha)^3 ( 2 \gamma - \beta - \alpha ) \).
以上でしたーお疲れ様です。