ブラベー格子の定義がいろんな参考書や記事を見ても、やたら難しい感じに書いてあると思ったので、小学生にでもわかるような表現をここに書こうと思ったのです。
ここでは7つの結晶系の分類の話はすっ飛ばします。多分それが分かんなくてもブラベー格子の定義は分かると思います。
強いて言えば、結晶とは何か、単位格子は全て平行六面体であることが分かってなきゃいけないかも。
ブラベー格子の定義
ブラベー格子の、めっっちゃ簡単な言葉で、しかも正確な表現は以下のようにできます。
ブラベー格子の定義
ブラベー格子では、どの原子から見ても、まったく同じ景色が広がる。
というのが定義です
これを踏まえて、下図、14種あるブラベー格子では、確かにどの原子の上に立っても景色が変わらないことを確認してほしいです。
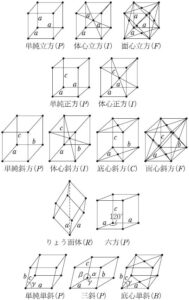
また、下の図のペロブスカイト構造というのがブラベー格子ではないこともすぐわかるでしょう。(まあ現実は同種の原子だけでできたペロブスカイトは無いかもしれませんが、例えばの話。)
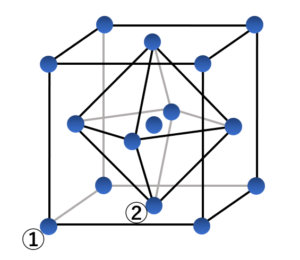
①と②の原子から見た景色は違うからです。①と②の上下の原子との距離が違いますね。
真ん中の原子さえ無ければ、面心立方格子となり、
どの原子から見ても同じ景色が広がる(ブラベー格子)でしょう。
また、次の疑問も簡単に解決できます。
なぜ単純、体心、底心、面心の4種類の配置なのか?
他は無いの?
まず、「どっから見ても同じ」という定義から、
単位格子の中で原子は、ある2つの原子を結ぶ中点にしか配置できません。
さもなければ、それらの片方の原子により近い、ということになり、定義に合いません。
ここまで配置を絞り込めたなら、単純、体心、底心、面心以外有り得ないことは
しらみつぶしに確かめて理解できるかと思います。
ただし、以下のことには注意しましょう。
- 体心と面心の両取り(?重ねたもの?)は
ペロブスカイト構造なので無効。 - 体心と底心の両取り(?重ねたもの?)は
ペロブスカイト構造と同じ理由でブラベー格子にはならない。
何か間違いがあれば、コメントを頂ければ幸いです。