この記事では1次元格子のタイトバインディング(tight-binding、強結合、強束縛)モデルでの状態密度を導出していきます。
もともと、1,2,3次元まとめて書こうかと思ったんですが、ばか長くなるので分けました
2次元についてはこちらの記事を読まれたら幸いです(3次元はそのうち書きます)
-
-
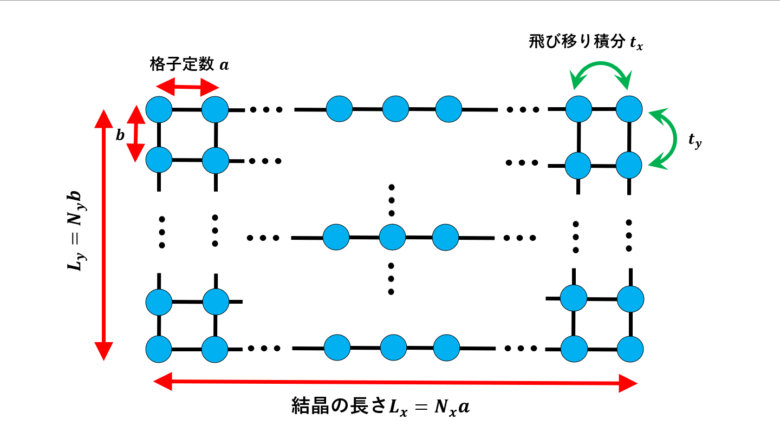
タイトバインディングモデルの状態密度(2次元長方格子)
2023/7/6
ここでは、2次元長方格子のタイトバインディングモデルでの状態密度を求めます。 1次元についてはこちらの記事を読まれたら幸いです。(3次元はそのうち書きます) 2次元長方格子のタイトバインディングモデル ...
タイトバインディング近似では、一次元格子の分散関係が
\( E(k) = 2t \cos(ka) \)
となることを前提知識として説明します。
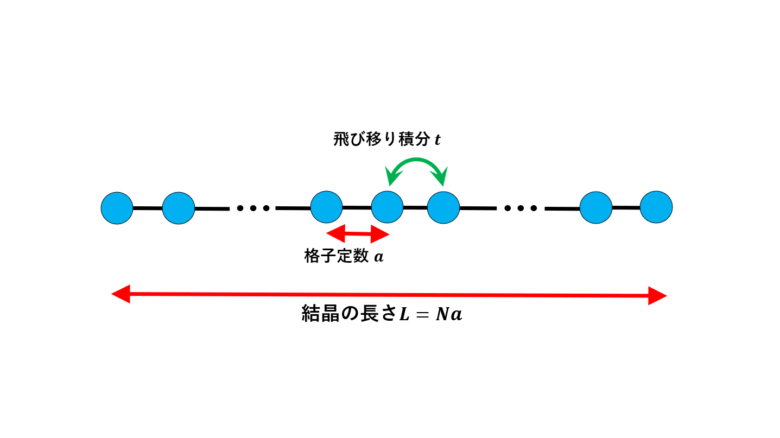
ここで注意して頂きたいのは、ここでは簡単に見えるために、クーロン積分(原子が孤立している場合のエネルギー固有値。よく\(E_0\) や \(\epsilon_0\) で表されかと思います。)を基準にエネルギー \(E(k)\) を測っていることです。また \(t\) は飛び移り積分(ホッピング)、\(a\) は格子定数です。(上の図)
また、結晶の長さ(周期境界条件の周期)を\( L=Na \) とします。
まず、(ブロッホ)波数が \([k, k+dk) \) と \([-k , -k+dk)~~~(k, dk >0 )\) の範囲にある状態の数 \( dN^* \)(\(L=Na\) の \(N\) とかぶらないために\(*\) を付けました。)は、
1つの状態が占める(ブロッホ)波数空間での長さは \( 2\pi/L \) ですから、
\( dN^* = 2 \times 2 \times dk / \left(\frac{2\pi}{L} \right)
\\~~~~~= 2 \displaystyle \frac{L}{\pi} \cdot \frac{dk}{dE} dE \)
2つの因子 \(2\) はそれぞれ、電子のスピン\( \uparrow, \downarrow \) の状態と、ブロッホ波数\(k\) が正と負の状態を同時に数えたことによるものです。
これと、\(k>0\) で
\( \displaystyle \frac{dE}{dk} = 2ta \sin(ka)
\\~~~~~= 2ta \sqrt{1- \cos^2(ka)}
\\~~~~~= a \sqrt{4t^2 - E^2}
\\ \Leftrightarrow \displaystyle \frac{dk}{dE} = \frac{1}{a \sqrt{4t^2 - E^2}} \)
であることから、
\( dN^* = 2 \displaystyle \frac{L}{\pi} \cdot \frac{1}{a \sqrt{4t^2 - E^2}} dE \)
以上から、状態密度 \(dN^*/dE\) は
1次元格子のタイトバインディングモデルの状態密度
\( \displaystyle \frac{dN^*}{dE} = \frac{2N}{\pi} \cdot \frac{1}{\sqrt{4t^2 - E^2}} \)
となります。(\(N=L/a\)使いました)
\( E = \pm 2t\) のところで発散するのですねー
そして格子定数 \(a\) に依存しないのですねー
まあ飛び移り積分 \(t\) が\(a\) に依存しそうですが。
読んでくださってありがとうございました。