なんだか2次元逆格子の基本並進ベクトルの公式が世に出回ってない気がしたので、
導出と合わせて書きます。
3次元逆格子の基本並進ベクトルの公式を前提知識としまして、それから2次元の公式を得ます。
2次元逆格子の基本並進ベクトルの公式
3次元の公式は以下に示す通りですね。
\( \vec{a^*} = 2\pi \displaystyle \frac{\vec{b} \times \vec{c}}{\vec{a} \cdot (\vec{b} \times \vec{c}) } \), \( \vec{b^*} = 2\pi \displaystyle \frac{\vec{c} \times \vec{a}}{\vec{a} \cdot (\vec{b} \times \vec{c}) } \), \( \vec{c^*} = 2\pi \displaystyle \frac{\vec{a} \times \vec{b} }{\vec{a} \cdot (\vec{b} \times \vec{c}) } \).
( もちろん \( \vec{a}, \vec{b}, \vec{c} \) と \( \vec{a^*}, \vec{b^*}, \vec{c^*} \) はそれぞれ実格子、逆格子の基本並進ベクトル )
2次元格子は、3次元格子で1つの基本並進ベクトルの長さが無限である(言い換えれば、ある方向に周期が無限である)場合だと見なすことができます。
よって \( \| \vec{c} \| \rightarrow \infty \) とすれば、(というか「逆格子ロッド」の存在を意識するためにそう考えるべき)
以下のように2次元逆格子ベクトルが得られます。
2次元逆格子ベクトルの公式
\( \vec{a^*} = 2\pi \displaystyle \frac{\|\vec{b} \|^2 \vec{a} ~ - ~ (\vec{a} \cdot \vec{b}) \vec{b}}{\| \vec{a} \times \vec{b} \|^2},
\\ \vec{b^*} = 2\pi \displaystyle \frac{\|\vec{a} \|^2 \vec{b} ~-~ (\vec{a} \cdot \vec{b}) \vec{a}}{ \| \vec{a} \times \vec{b} \|^2}. \)
もちろん、\( \vec{a^*} \cdot \vec{a} = \vec{b^*} \cdot \vec{b} = 2 \pi,~~~ \vec{a^*} \cdot \vec{b} = \vec{b^*} \cdot \vec{a} = 0 \) です。
より具体的な導出、あるいは逆格子ロッドが何なのか気になる方は以下に書きますので、読まれたら嬉しいです。
公式の導出、逆格子ロッドとは
\( \| \vec{c} \| \rightarrow \infty \) とする前にまず、
\( \vec{c} \) を3つの一次独立なベクトル \( \vec{a}, \vec{b}, \vec{a} \times \vec{b} \) の方向に分解します。
\( \vec{c} = \alpha ~\vec{a} + \beta ~\vec{b} + L ~\vec{n} \).
ここで \( \vec{n} = \displaystyle \frac{ \vec{a} \times \vec{b} }{ \|\vec{a} \times \vec{b}\| } \) は \( \vec{a}, \vec{b} \) が張る平面に垂直な単位ベクトルです。
この \( \vec{c} \) を3次元の \( \vec{a^*}, \vec{b^*}, \vec{c^*} \) の式に代入すると、
\( \vec{a^*} = 2\pi \displaystyle \frac{\|\vec{b}\|^2 \vec{a} ~-~ (\vec{a} \cdot \vec{b}) \vec{b}}{\| \vec{a} \times \vec{b} \|^2} ~ + ~ 2\pi \frac{\alpha}{L}~\vec{n} \),
\( \vec{b^*} = 2\pi \displaystyle \frac{\|\vec{a}\|^2 \vec{b} ~-~ (\vec{a} \cdot \vec{b}) \vec{a}}{\| \vec{a} \times \vec{b} \|^2} ~-~ 2\pi \frac{\beta}{L}~\vec{n} \) ,
\( \vec{c^*} = \displaystyle \frac{2\pi}{L} \vec{n} \).
ここで、ベクトル解析の公式
\( \vec{A} \times (\vec{B} \times \vec{C}) = (\vec{A} \cdot \vec{C})~\vec{B} ~-~ (\vec{A} \cdot \vec{B})~\vec{C} \)
などを使いました。
\( L\) が無限に大きい、つまり\( \|\vec{c}\| \rightarrow \infty \) とすると、
( \(\alpha, \beta \) は無限に大きくなくても、どっちでもええわ)
\( \vec{c^*} \) は無限に短いが(長さ=0)、方向 \( \vec{n} \) を持つ基本並進ベクトルとなります。
そして、上式の3次元空間で基本並進ベクトル \( \vec{a^*}, \vec{b^*}, \vec{c^*} \) による逆格子は、
格子点というか格子線?といいますか、直線の集まりになってしまいますね。
そいつらを逆格子ロッドと呼びます。
電子線やX線回折での結晶構造の解析の話であれば、
2次元試料に入射したX線などの散乱ベクトル \( \Delta \vec{k} = \vec{k'} - \vec{k} \) が、この逆格子ロッド上の任意の点が表すベクトルであるときに回折が起きます。
(バンド理論からこの記事にやって来た人たちは、この言ってる意味が分からんくてもいいんじゃないかと。)
そして、先に示した2次元の \( \vec{a^*}, \vec{b^*} \) の公式
\( \vec{a^*} = 2\pi \displaystyle \frac{\|\vec{b}\|^2 \vec{a} ~ - ~ (\vec{a} \cdot \vec{b}) \vec{b}}{\| \vec{a} \times \vec{b} \|^2} \), \( \vec{b^*} = 2\pi \displaystyle \frac{\|\vec{a}\|^2 \vec{b} ~-~ (\vec{a} \cdot \vec{b}) \vec{a}}{\| \vec{a} \times \vec{b} \|^2} \)
は、あくまで、この逆格子ロッドを垂直に切ったとき、つまり \( \vec{a}, \vec{b}\) が張る面内で切ったときにできる格子点の基本並進ベクトルです。
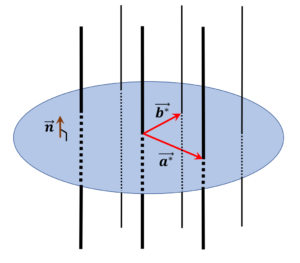
ちなみにバンド理論の話だったら単純に、
逆格子ロッドの波数ベクトルの中から、2次元面に垂直な結晶運動量=0になるものだけブロッホ波数として取り出したのが上の公式、と解釈すればいいんでしょう。
何か間違っているところがあれば、コメントを頂ければ幸いです。