-

-
Oracle 名前付きロック(アドバイザリロック)の取得方法
Oracleで名前付きロック(アドバイザリロック)を現場で使う必要があったので、忘備録です。 具体的には、DBMS_LOCKパッケージを使った名前付きロックの取得と解放のやり方をメモします。 SQLの ...
-

-
Microsoft Businessのアカウントの削除方法
2023/8/30
私は最近、短い期間だけMicrosoftのたくさんのアプリを使う必要に迫られ、できれば無料で使いたかったので、 Microsoft Business Standard というプランを1ヶ月無料で試すこ ...
-
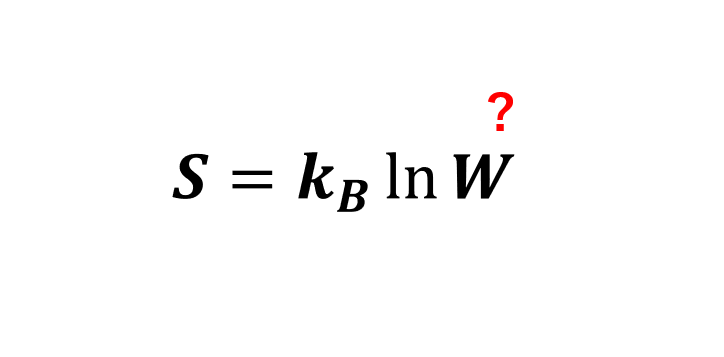
-
状態数とは?エントロピーの式の正確な意味
2023/7/19
エントロピーの式 \( S(E) = k_B \ln W(E) \) (温度\(T\)とかにも依存するかもしれないですが、省きます。)において、「状態数」\(W(E)\)というものが出てきますが、 私 ...
-
-
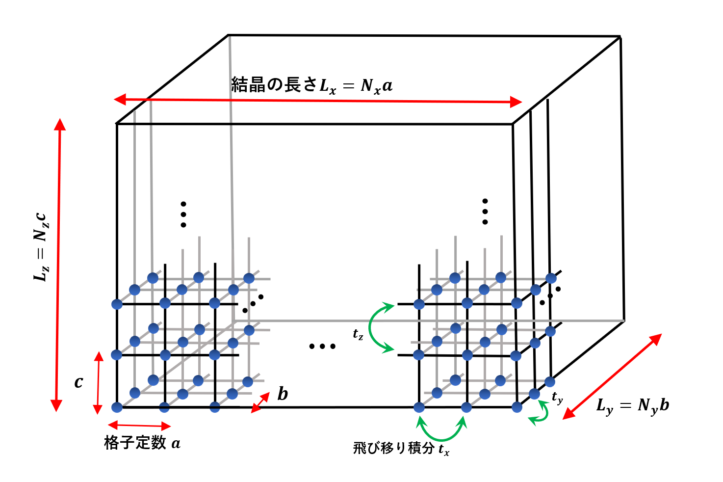
タイトバインディングモデルの状態密度(3次元斜方格子)
2023/7/24
ここでは、3次元斜方格子(直方格子)のタイトバインディングモデルでの状態密度を求めます。 1、2次元についてはこちらの記事を読まれたら幸いです。 3次元斜方格子のタイトバインディングモデルの状態密度 ...
-
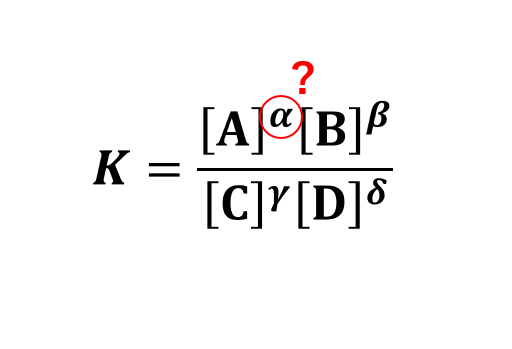
-
平衡定数-なぜ係数乗?係数と平衡定数の関係を直観的に説明
2023/7/10
むかしむかし、高校の化学の平衡定数\( K \) について、なぜに反応式の「係数乗」出てくんねん、と思ったので、考えたら直観的な説明が作れました(と思います)。 あと、なかなか直観的に説明している記事 ...
-
-
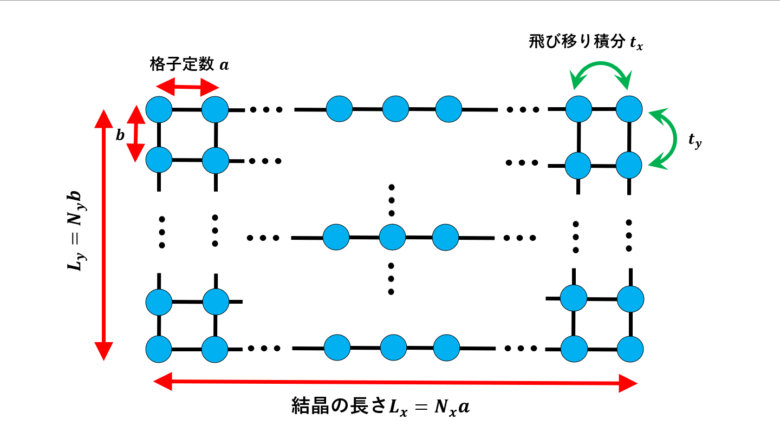
タイトバインディングモデルの状態密度(2次元長方格子)
2023/7/6
ここでは、2次元長方格子のタイトバインディングモデルでの状態密度を求めます。 1次元についてはこちらの記事を読まれたら幸いです。(3次元はそのうち書きます) 2次元長方格子のタイトバインディングモデル ...
-
-
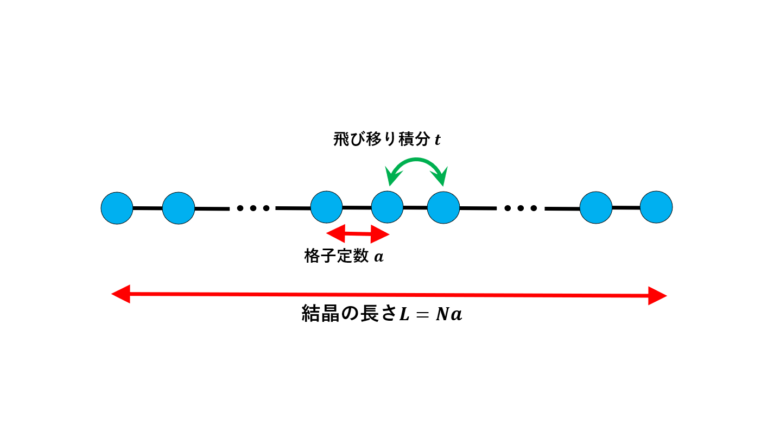
タイトバインディングモデルの状態密度(1次元格子)
2023/7/4
この記事では1次元格子のタイトバインディング(tight-binding、強結合、強束縛)モデルでの状態密度を導出していきます。 もともと、1,2,3次元まとめて書こうかと思ったんですが、ばか長くなる ...
-
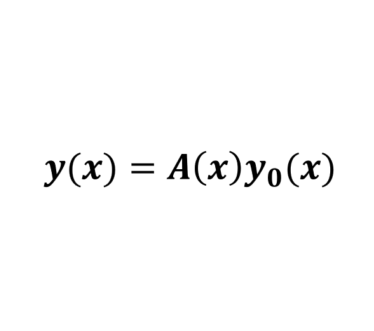
-
定数変化法でなぜ微分方程式が解けるのか?一般性が失われないことについて
2023/7/4
むかし大学生のときに、微分方程式の定数変化法について、 こんなことをしていいのか、これで本当に一般解が求められているのか と考えたことがある。 一度分かってしまえば、当然のことであるようなことなのだが ...
-
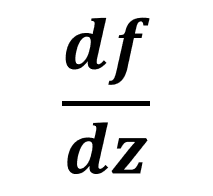
-
複素関数の微分~コーシーリーマンの関係式のいちばん直観的な導出
2023/6/16
ここでは、複素数の関数の微分に興味を持った方のために、それがどんなものかと、 複素関数が微分できるための条件となる、コーシーリーマンの関係式の導出をします。(「証明」じゃなくて「導出」って言いたい) ...
-
-
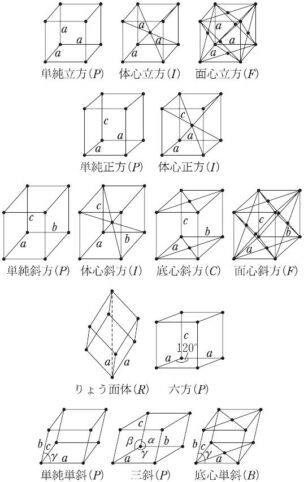
ブラベー格子とは?なぜ単純、体心、底心、面心の4種類?分かりやすく、簡単な言葉で
ブラベー格子の定義がいろんな参考書や記事を見ても、やたら難しい感じに書いてあると思ったので、小学生にでもわかるような表現をここに書こうと思ったのです。 ここでは7つの結晶系の分類の話はすっ飛ばします。 ...